Data Inversion: Theory

Data inversion algorithms

We use the method of inversion with regularization with constraints, which has evolved into the standard method for the retrieval of microphysical parameters of tropospheric particles from multiwavelength lidar observations. Profiles of the physical particle properties follow from the numerical inversion of the vertically and spectrally resolved particle backscatter and particle extinction coefficients. The optical data are related to the physical quantities through Fredholm integral equations of the first kind:

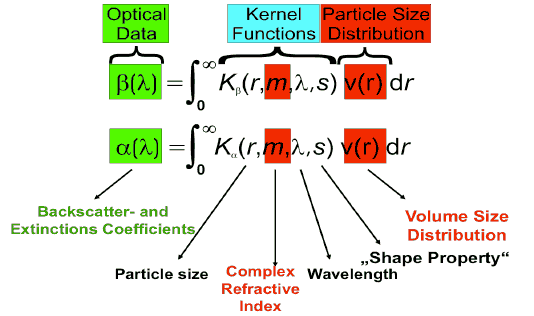
The backscatter and extinction coefficients measured with Raman lidar serve as input to the integral equations shown on the right-hand side. Each measurement of a 3+2 Raman lidar consists of profiles of 3+2 data sets. In practical application we solve the equations for each height layer and in this way we obtain profiles of the investigated microphysical parameters.

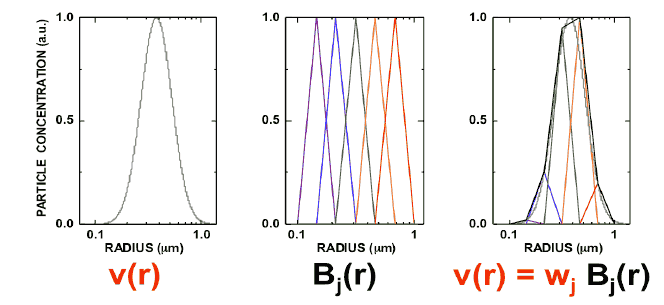
Volume distributions of atmospheric aerosols can be approximated by so-called logarithmic-normal distribution; they have a Gaussian-like shape when we use a logarithmic particle radius scale. We solve the above equations for the volume size distribution. In practical application this means that we must approximate the volume size distributions by a linear combination of base functions B_j(r) weighted with their weight factors w_j. The linear combination of triangle functions with their respective weight factors then provides us with the approximation of the investigated particle size distribution.

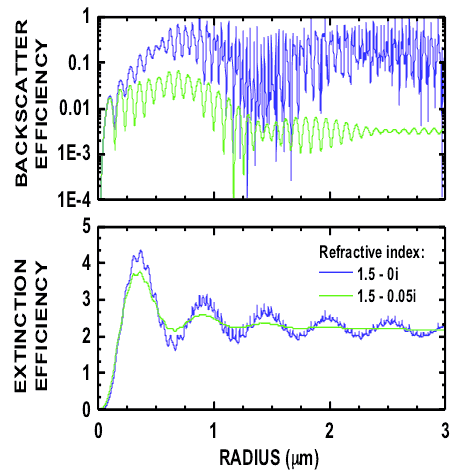
The kernel functions describe the light-scattering properties of individual particles of radius and complex refractive index and a specific wavelength.

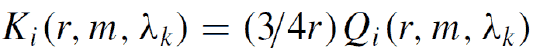
The main component of these kernel functions are the backscatter and extinction efficiencies Q_i(r,m,λ_k). If we assume spherical particle shape we can apply Mie-scattering theory to compute these efficiencies. The plot below shows two examples of backscatter and extinction efficiencies for particles up to 3 mm in radius. The efficiencies were computed under the assumption of a particle complex refractive index of 1.5 (real part) – 0i (imaginary part) and 1.5 – 0.0i. The first case describes non-absorbing particles. In the second case, the imaginary part of 0.05i describes strongly light-absorbing particles.