Is there a place for rote learning multiplication tables in English primary schools?

Dr LizAnn Petch - Current University of Hertfordshire student

Abacus

Abstract

Recent neurological studies give new insights into learning, including memorising and recall. These new discoveries have not been considered from the viewpoint of what they might contribute to the understanding of rote learning. The relevant findings of these studies are discussed and their implications for rote learning multiplication facts are presented in this article. In my judgement the commonly-held view that rote learning is not an appropriate tool for mathematics learning should be reconsidered.

Introduction

Changes to the National Curriculum that came into effect in September 2014 require that by the end of Year 4 (age 9) children know all the multiplication facts up to 12 × 12 (Department for Education, 2013). This is more information, and by a younger age, than prescribed in earlier versions of the National Curriculum in England and Wales. The non-statutory guidance advises that children are introduced to tables, and that they practise to recall facts and become fluent, but offers no suggestions for teachers, parents, or the pupils themselves, as to how this might be achieved.

Until about 40 years ago, rote learning (typically the whole class chanting the tables out loud) was the usual method of learning tables. After the Plowden Report (Central Advisory Council for Education (England) 1967) this practice was discontinued in English schools.

Recent neurological research has increased knowledge about how the brain works. There is now greater understanding of how short- and long-term memory relate to the learning, memorising and use of number facts. I have decided to focus on how this understanding of brain function, together with the processes of rote learning, may be used to support children as they learn multiplication tables.

Political context

For many years education has been high on the political agenda, particularly since Tony Blair replied 'Education, Education, Education' when asked during the 1997 General Election campaign for the three most important concerns for a prospective Labour government. Recently Michael Gove, when Education Secretary, prompted much debate among those concerned with mathematics education. Changes he made to the mathematics curriculum from September 2014 (Department for Education, 2013) elicited a powerful and widespread response. Criticism of these changes by many respected education professionals (Bassey et al., 2013) suggested that only by rote learning could the increased content of the curriculum be taught. Denigration of rote learning was used to support their view that the curriculum was overloaded. In my opinion, this also sustains the taboo in England against rote learning which has hidden its potential.

'Rote learning' is the method of learning multiplication tables by repeating whole multiplication facts (e.g. 2 × 4 = 8) not just step-counting (e.g. 2, 4, 6, 8) many times until they can be recalled accurately. The important details of this repetition: the words used; the number of facts processed at one time; the time spent each session; the intervals between sessions; the balance between testing and learning, etc. will be considered later. Three words - recall, recognise and remember - are used to describe what happens when multiplication facts devoid of context (other than that of multiplying integers) are given when requested. These appear in Krathwohl's revision (2002) of Bloom's taxonomy (1956), and correspond to Bloom's positioning of knowledge at the first level of his taxonomy (Figure 1).

Fig 1

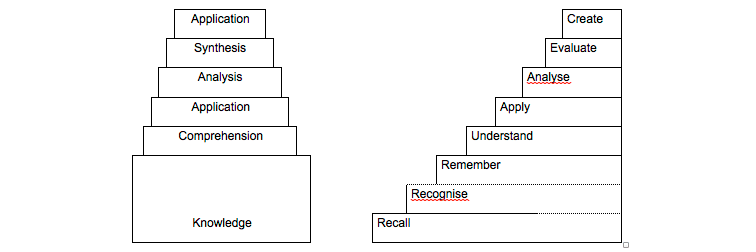
Fig. 1 Bloom's Taxonomy (1956) (left) and Krathwohl's revised Taxonomy (2002) (right)

'Knowledge' of multiplication tables is used now (Fitt, 2015) to convey the higher order attributes 'Understand' and 'Apply' in Krathwohl's taxonomy. I therefore suggest that this implies that 'Recall', 'Recognise' and 'Remember' describe the ability to say, write, or recognise correct multiplication facts such as 2 × 3 = 6. In the same way, I suggest that 'Knowledge', 'Understand' and 'Apply' can all be used to describe the ability to use multiplication concepts as well as facts in increasingly complex contexts, such as 'Two children have three apples each. How many apples are there altogether?'. Care must be taken, therefore, both in asking questions and interpreting the answers. So the question 'Do you know your tables?' could be interpreted by the respondent for example as 'Can you recall your tables?' or 'Do you understand what multiplication tables can mean?' and their answer may reflect this significant difference.

Memorising is considered to be effective when the required material can be recalled both accurately and immediately on demand. The terms 'fluency' and 'automaticity' are used together to define this (Dougherty and Johnston, 1996). Fluency describes the accuracy and clarity with which the recall is achieved. Automaticity describes the situation in which recall is achieved without apparent conscious thought: this recall is said to be best developed by drill and practice (Hasselbring, 1988).

Whatever the method of achieving it, automaticity with basic facts is claimed to reduce anxiety about mathematics (Poncy et al., 2007; Parkhurst et al., 2010) and increase general confidence in mathematics (Bahrick and Hall, 1991). Automaticity may also enhance the acquisition of more complex skills. This may be achieved either by freeing up general cognitive capacity, or when accuracy of the basic facts recalled automatically is a component of a more complex task (Poncy et al., 2007).

I will put these findings, together with my review of relevant neurological studies into the context of learning multiplication facts later in this article.

Current ideas and practice

'Mathematics in the Primary School' (Skemp, 1989) is still widely used as a key text in the education and training of primary school teachers. More recent texts, for example 'Transforming Primary Mathematics' (Askew, 2012) continue the discussion of both theory and practice of teaching and learning mathematics.

Skemp distinguishes between two fundamentally different learning styles. 'Habit learning' is characterised by memorising and recall of facts and algorithms which may be applied to subsequent tasks. He describes 'Intelligent learning' as grounded in its context, but also adaptable to other circumstances. I consider that 'Habit learning' describes the 'Recall, Recognise and Remember', and 'Intelligent leaning' corresponds to 'Understand and Apply' in Krathwohl's taxonomy. Skemp clearly indicates throughout his book the desirability of 'Intelligent learning' where possible, though he does acknowledge that 'Habit learning, with rote learning as a special case, can be useful and necessary, even in mathematics' (Skemp, 1989). He does discuss the advantages of being able to carry out a mathematical procedure, once understood, with a minimum of conscious thought (more usually described now as cognitive load). In my view this is essentially what others (Dougherty and Johnston, 1996) describe as automaticity and fluency. Skemp makes it clear that, in his view, this development of automaticity is fundamentally different from that achieved by simple repetition without understanding.

Askew's later book (2012) continues the discussion about how young children learn mathematics in terms of activities shared by the children and their teacher. He describes children and their teacher taking part in 'Activities' (such as learning about multiplication) which consist of several 'Actions' (including, for example, recalling multiplication facts) which cannot be isolated from the whole. In my opinion the tone of Askew's book implies that this 'new mathematics' he endorses (p. xi) corresponds to the 'knowledge with understanding' style of learning Skemp describes. Askew asserts that 'While there is a place for some skills, they are a small part of the mathematics repertoire children now need' (p. 25). He does not identify specifically what these skills might be, but comments that if children know that 8 + 2 = 10, this opens the door to further exploration of addition (p. 53). I suggest that recall of multiplication facts is one of these specific skills, and in the same way this recall opens the door to further exploration of multiplication. I suggest further that these skills correspond to Skemp's 'Habit learning' and which I identify as rote learning.

I will use my consideration of studies of brain function to suggest that rote learning multiplication facts (the Habit learning Skemp denigrates, and Askew admits to using himself (p. 6)) may have a significant place in the classroom. Efficient rote learning may offer one action in the whole activity of studying multiplication.

Brain structure, memory and recall

The initial response by the brain to any type of stimulus is thought to be a change in the network of connections between neurons (the basic nerve cells in the brain). This change is the result of chemical activity by neurotransmitters in the synapses that form the connections. (Synapses are the spaces between the ends of neurons.) Further biochemical processes allow repeated activity to produce long-lasting changes in how the synapses link adjacent neurons, strengthening their connection. This repetition and the security it gives to the network of neurons (neurological pathways) are seen as key features in the whole learning process of memorising and recall (Watson et al., 2010; Sousa, 2003).

Types of memory

Three main types of memory have been identified and compared (Cowan, 2008).

Short-term memory in the hippocampus holds a relatively small amount of information for a few seconds. Information held here is subject to temporal decay and capacity overload - it can be quickly lost (forgotten) and only a small, fixed amount can be held. It has been suggested that short-term memory capacity increases dramatically between pre-school age and adolescence (Gathercole, 1999).

Long-term memory is a vast store of knowledge and a record of prior events which are available for recall, and it is not subject to these limitations: it may be stored indefinitely and has apparently unlimited capacity. Information is sent to one or more of the long-term storage areas in the brain - usually in the cortex - by the hippocampus.

Working memory is a short-term memory applied to cognitive tasks: it is a multi-component system that holds and manipulates information in a short-term memory. It also controls attention in order to manage the short-term memory.

It is thought (Gathercole, 1999) that both the complex working memory and the capacity to retain information in the long-term memory also increase considerably between pre-school and adolescence. Gathercole considers that this may be because many processes in the brain including the construction and maintenance of memory traces (neurological pathways) are developing. I think that this theory may offer evidence to support the idea that the primary school years - when children are near the beginning of this spurt in brain development - are a good time to learn multiplication tables by rote, taking advantage of the development of neurological pathways during this time.

Activity in the brain during memorisation

The development of functional Magnetic Resonance Imaging (fMRI) technology during the 1980s enabled the study of electrical activity in the brain while a research subject carried out a task. The structures involved and interaction between them could then be identified.

The transfer of an episodic memory from the hippocampus (short-term memory) to the cortex (long-term memory) from which it can be retrieved later is the neurological description of memorising. This is one of the principal processes being considered in this study. Learning multiplication facts has been shown to involve a shift from processing numbers (e.g. carrying out repeated addition) to more automatic retrieval (Ischebeck et al., 2006). Ischebeck's study also suggested that memorising and recall use two different neural pathways, one for rote learning and one for learning with understanding. Responses to questions about this learning also use the two different neural pathways. I consider this to be a very important finding, as it suggests that using both of the different neural pathways to memorise and recall multiplication facts may be efficient and effective.

Cognitive processing theories (Delazer et al., 2003) indicate that the brain's cognitive capacity is limited, and carrying out several tasks at once is difficult. It has been suggested that increasing automaticity, which requires little conscious effort, may free up cognitive resources that can be applied to a more complex task being attempted simultaneously (Dehaene and Cohen, 1997; McCallum et al., 2006). These studies offer some evidence that both fluency and automaticity are achieved when the information is understood sufficiently to be stored in the long-term memory and available for recall. Another suggestion they make is that information can be stored in the long-term memory without full understanding. In my opinion rote learning - repetition until the material can be accurately recalled - may achieve this. Rote learning has been criticised as learning without understanding, but this very feature is acknowledged here, and memorising can still be achieved. It is further suggested that these two routes to memory are different and the routes of recall are also different: the situation requiring the recall may dictate the recall pathway. In my view this is further support for the use of rote learning multiplication tables. Memorising multiplication facts without full understanding does not prevent or even limit their recall and use, and using these facts has been shown to promote later understanding.

A recent longitudinal study (Qin et al., 2014) monitored the activity in the brains of children between the ages of 7 and 9 years while they carried out single-digit addition and multiplication. The researchers found that as these children developed, the activity recorded in the hippocampus increased while that in the relevant area of the cortex decreased.

How much can be memorised

Understanding how much can be 'taken in' at any one time has been gained from work reported in the 1950s (Miller, 1956) and developed in the 1970s (Simon, 1974). Both authors proposed the notion of 'chunks' of information as the units of stimulus material that could be held in the short-term memory. Research showed that the number of pieces of information – unrelated numbers, letters, words, etc - was fairly constant across all ages and cultures of healthy young people and adults. Miller (1956) reported this as the 'Magic Number Seven' and suggested that this was the maximum number of items that could be successfully memorised in one session.

Recall

Research in the 1980s (Stazyk et al., 1982; Ashcraft, 1987; Campbell and Graham, 1985) into how children learn basic arithmetic skills was entirely focused on the retrieval or recall (giving the correct response) rather than the acquisition of the multiplication facts, and considered the extent to which a back-up strategy (typically repeated addition or comparison with a known multiplication, addition, or other fact) contributed to the speed and accuracy of a correct response. A study of children's improvement in recall after practice (Siegler, 1988) showed that recall (there described as retrieval directly from memory) was not only faster but also more accurate than when back-up strategies were used. In my opinion this is a fundamental assertion about recall, suggesting that learning facts alone leads to more successful retrieval than using back-up strategies involving understanding. I think that it can be inferred from this that rote learning of multiplication facts devoid of specific context allows accurate and rapid retrieval (fluency and automaticity) while back-up strategies develop understanding rather than speed. I suggest that this makes a very good case for including rote learning of multiplication tables in the primary classroom because it complements learning with understanding.

Another report published in the same year (Ter Heege, 1985) suggests that the development of informal thinking strategies - the back-up strategies described by the earlier accounts - supports learning by heart, and will eventually result in fluency and automaticity. The question not posed in Ter Heege's article (1985), however, is why should rote learning not be used as well to achieve fluency and automaticity more quickly and easily? Successful recall and understanding are both requirements of the National Numeracy strategy. I think that both techniques - rote learning for recall and other, varied strategies for understanding - should be used in the classroom.

Effective memorisation

If techniques are being considered to ensure that multiplication facts are memorised - transferred from short-term to long-term memory - and available for recall, then it is important that they are both effective and efficient. Whole class chanting of tables in English schools many years ago was certainly not informed by any knowledge of how children learn, but research is indicating how repeated recitation of facts to be learned can be done effectively and that frequent testing actually improves recall (Roediger and Karpicke, 2006).

Research into the intervals between studying items to be learned showed that learning was more effective when the study sessions were more spaced out (Hintzman, 1974). This spacing effect is further enhanced if the intervals between the sessions are gradually increased. A study of primary-age children learning multiplication facts and spelling lists - topics very relevant to this review - indicated that children could recall twice as many multiplication facts when the study sessions were timed in an expanded series than when the same amount of study time was used in one session (Rea and Modigliani, 1985). (An expanded series is one in which the intervals between each study session increase every time.) A study of memorisation and recall of new vocabulary (Bahrick and Phelphs, 1987) suggested that the best recall is achieved when the intervals between study sessions are those which are the longest that do not result in forgetting. They found that only about seven study sessions were needed to achieve almost complete recall of the required material.

It has also been shown (Roediger and Butler, 2011) that frequent testing, where strong effort is made to recall the required fact before feedback (the correct response) is given, actually improves recall. It is suggested that the effort of recollection strengthens the neural pathways involved in memorisation.

I suggest that these two important findings, described by different research teams (cited above) with different priorities, could be used together to support children as they learn multiplication facts. Gradually increasing the time between study sessions and frequent testing (not just rehearsing) have both been shown to improve performance. I think there is an opportunity to use these findings to inform the development of efficient strategies for rote learning multiplication tables.

I consider that, taken together, the studies of brain structure and function, and strategies for learning and recall described above suggest that rote learning multiplication tables, far from being 'anathema to the ideals of progressive education as it is unnatural, unpleasant and laborious' (Didau, 2014)may have a place in English primary schools, grounded in evidence-based research.

Conclusion

My review of the literature has indicated that there has been very little work done to combine research findings from neurological studies with those from rote learning of multiplication tables, even though neuroscience does offer considerable insight into learning.

I have identified six key findings in neurological studies which I think have substantial implications for how the process of rote learning may be understood and used:

Facts and concepts are stored independently in the brain, and also recalled independently by the use of their own separate neurological pathways. This suggests to me that rote learning could be undertaken at the same time as activities to develop understanding without conflict or confusion.
Facts can be memorised without understanding. This does not affect their later recall and actually supports the subsequent development of understanding. It would seem that multiplication tables may be learned by rote and their later recall used to support understanding.
Enhancing automaticity frees up cognitive resources that can be used in a more complex task. Multiplication facts which are recalled automatically do not take up cognitive resources being used to develop conceptual understanding: the facts may actually support the understanding.
Effort made to recall facts without context before resorting to back-up strategies strengthens memory.
Recall of facts stored without understanding has greater fluency and automaticity than recall using understanding.
A small number of related facts can be memorised quickly and efficiently using simple techniques. These methods involve: repeating about six related facts several times; rehearsing these facts at increasing intervals; testing recall for fluency and automaticity. These techniques lend themselves particularly well to the effective rote learning of multiplication tables.

These key findings are closely linked to each other and inform both rote learning and learning with understanding. I have shown this interconnection as a conceptual framework in Figure 2. A circle illustrating the close relationship between rote learning and learning with understanding is at the centre. It is surrounded by a ring comprising six sections which represent the points above. The ideas in these sections all contribute to understanding about rote learning and learning with understanding. This format indicates effectively the close relationship I postulate between the two styles of learning and the neurological findings. I think that the overarching question posed at the beginning of this paper 'Is there a place for rote learning multiplication tables in the English primary classroom?' has been answered very clearly, as my consideration of the literature indicates good neurological evidence to support the practice of rote learning in conjunction with learning with understanding.

Fig 2

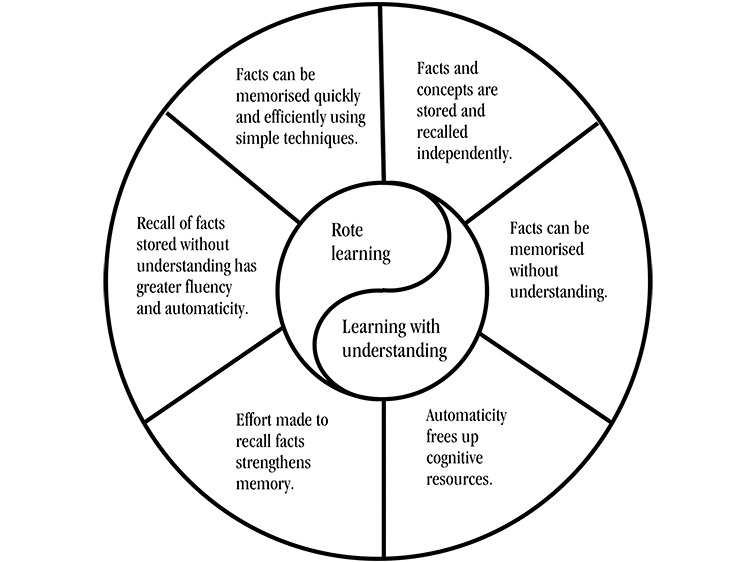
Fig. 2 Diagram illustrating the six key neurological findings which contribute to understanding of rote learning and learning with understanding – a conceptual framework.

⇠ Read 'Reframing spaces...'Read 'Assess compassion in Higher Education...' ⇢

References

Ashcraft, M. H. (1987) Children's knowledge of simple arithmetic: A developmental model and simulation. Formal methods in developmental psychology. New York: Springer.
Askew, M. (2012) Transforming Primary Mathematics. Abingdon: Routledge.
Bahrick, H. P. and Hall, L. K. (1991) 'Lifetime maintenance of high school mathematics content'. Journal of experimental psychology: general, 120 (1), pp.22-33.
Bahrick, H. P. and Phelphs, E. (1987) 'Retention of Spanish vocabulary over 8 years'. Journal of Experimental Psychology: Learning, Memory, and Cognition, 13, pp.344-349.
Bassey, M., Wrigley, T., Maguire, M., Pring, R., Goldstein, H. and others. (2013) 'Letters - Gove will bury pupils in facts and rules'.[Online]. Available at: http://www.theguardian.com/politics/2013/mar/20/gove-curriculum-dumb-down-education [Accessed: 13 January 2015].
Bloom, B.S. and Krathwohl, D.R. (1956) Taxonomy of Educational Objectives: The classification of educational goals. Handbook 1: cognitive domain.
Campbell, J. I. and Graham, D. J. (1985) 'Mental multiplication skill: Structure, process, and acquisition'. Canadian Journal of Psychology/Revue canadienne de psychologie, 39, pp.338-366.
Central Advisory Council for Education (England) (1967) Children and their Primary Schools : a report of the Central Advisory Council for England, HM Stationery Office.
Cowan, N. (2008) 'What are the differences between long-term, short-term, and working memory?' Progress in brain research, 169, pp.323-338.
Dehaene, S. and Cohen, L. (1997) 'Cerebral pathways for calculation: Double dissociation between rote verbal and quantitative knowledge of arithmetic'. Cortex, 33, pp.219-250.
Department for Education (2013) The national curriculum in England. Key stages 1 and 2 framework document. [Online]. London. Available at: https://www.gov.uk/government/uploads/system/uploads/attachment_data/file/335133/PRIMARY_national_curriculum_220714.pdf [Accessed 24 January 2015].
Delazer, M., Domahs, F., Bartha, L., Brenneis, C., Lochy, A., Trieb, T. and Benke, T. (2003) 'Learning complex arithmetic—an fMRI study'. Cognitive Brain Research, 18, pp.76-88.
Didau, D. (2014) 'I love rote learning'. [Online]. Available at: http://www.learningspy.co.uk/learning/♥-rote-learning/#more-6427 [Accessed 24 January 2015].
Dougherty, K. M. and Johnston, J. M. (1996) 'Overlearning, fluency, and automaticity'. The Behavior Analyst, 19 (2), pp.289-292.
Fitt, V. (2015) Conversation with EAP about rote learning. Professional conversation: 6 January 2015.
Gathercole, S. E. (1999) 'Cognitive approaches to the development of short-term memory'. Trends in cognitive sciences, 3, pp.410-419.
Hasselbring, T. S. (1988) 'Developing math automaticity in learning handicapped children: The role of computerized drill and practice'. Focus on Exceptional Children, 20, pp.1-7.
Hintzman, D. (ed.) (1974) 'Theoretical implications of the spacing effect.' Theories in cognitive psychology: The Loyola Symposium.
Ischebeck, A., Zamarian, L., Siedentopf, C., Koppelstätter, F., Benke, T., Felber, S. and Delazer, M. (2006) 'How specifically do we learn? Imaging the learning of multiplication and subtraction'. Neuroimage, 30, pp.1365-1375.
Krathwohl, D.R. (2002) 'A revision of Bloom's taxonomy: An overview'. Theory into practice, 41, pp.212-218.
McCallum, E., Skinner, C. H., Turner, H. and Saecker, L. (2006) 'The taped-problems intervention: Increasing multiplication fact fluency using a low-tech, classwide, time-delay intervention'. School Psychology Review, 35 (3), pp419-434.
Miller, G. A. (1956) 'The magical number seven, plus or minus two: some limits on our capacity for processing information'. Psychological review, 63, p.81 - 97.
Parkhurst, J., Skinner, C. H., Yaw, J., Poncy, B., Adcock, W. and Luna, E. (2010) 'Efficient class-wide remediation: Using technology to identify idiosyncratic math facts for additional automaticity drills'. International Journal of Behavioral Consultation and Therapy, 6 (2), 12, pp.111-123.
Plowden, B. B. H. P. (1967) Children and Their Primary Schools: a report of the Central Advisory Council for Education, HM Stationery Office.
Poncy, B. C., Skinner, C. H. and Jaspers, K. E. (2007) 'Evaluating and comparing interventions designed to enhance math fact accuracy and fluency: Cover, copy, and compare versus taped problems'. Journal of Behavioral Education, 16, pp.27-37.
Qin, S., Cho, S., Chen, T., Rosenberg-Lee, M., Geary, D. C. and Menon, V. (2014) 'Hippocampal-neocortical functional reorganization underlies children's cognitive development'. Nature neuroscience, 17, pp.1263-1269.
Rea, C. P. and Modigliani, V. (1985). The effect of expanded versus massed practice on the retention of multiplication facts and spelling lists. Human Learning: Journal of Practical Research and Applications, 4, pp.11-18.
Roediger, H. L. and Butler, A. C. (2011). The critical role of retrieval practice in long-term retention. Trends in cognitive sciences,15, pp.20-27.
Roediger, H. L. and Karpicke, J. D. (2006). Test-enhanced learning taking memory tests improves long-term retention. Psychological science, 17, pp.249-255.
Siegler, R. S. (1988). Strategy choice procedures and the development of multiplication skill. Journal of Experimental Psychology: General, 117 (3), pp.258-275.
Simon, H. A. (1974). How big is a chunk. Science, 183 (4142), pp.482-488.
Skemp, R. R. (1989). Mathematics in the Primary School, London, Routledge.
Sousa, D. A. (2003). How the Gifted Brain Learns, Thousand Oaks, California, Corwin Press, Inc.
Stazyk, E. H., Ashcraft, M. H. and Hamann, M. S. (1982). A network approach to mental multiplication. Journal of Experimental Psychology: Learning, Memory, and Cognition, 8 (4), pp.320-335.
Ter Heege, H. (1985). The acquisition of basic multiplication skills. Educational Studies in Mathematics, 16, pp.375-388.
Watson, C., Kirkcaldie, M. and Paxinos, G. (2010). The brain: an introduction to functional neuroanatomy, Academic Press.