Radial velocity

Stars with planets aren't stationary

We often picture our Solar System with the Sun in the middle, completely stationary, while all the planets move around it. However, this isn’t true – in reality, the planets and the Sun orbit their common centre of mass. This is most easily pictured by considering just one planet orbiting a star.

In this situation, the centre of mass will lie somewhere between the centre of the star and the centre of the planet. As the star is always more massive that the planet, the centre of mass will always lie closer to the centre of the star (this point often lies inside the star itself but displaced slightly from its centre). This means that the circular or elliptical path the star follows will be shorter than that of the planet and so the star will move slower too. The important thing to note though, is that the star does move.

The star's movement towards and away from us causes its light to be Doppler shifted. If these small variations of the star's light change in a regular pattern, then that may be evidence of a planetary companion!

Where is the centre of mass?

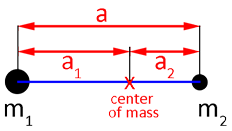Imagine the Earth is the only planet orbiting the Sun, at the same distance and speed that it currently does. With respect to the diagram, m2 represents the mass of the Sun and m1 the mass of the Earth. The centre of mass is defined such that m1a1=m2a2. Using the fact that a=a1+a2, it is possible to rearrange the above equation into the following form:

a2 = (m1a)÷(m1+m2)

Given that the mass of the Earth is approximately 6×1024kg, the mass of the Sun is 2×1030kg, and their separation is equal to 1 Astronomical Unit (1.5×1011m), find the distance between the centre of the Sun and the centre of mass.

How fast does the Sun move due to the Earth?

Now we know the radius of the Sun's orbit about the centre of mass we can find it's speed using the simple formula: speed = distance ÷ time.

For the time, we will use 1 year. In this time the Earth and Sun both orbit their centre of mass once, completing one circle. This means that the distance we must use is the circumference of a circle of radius a2 which is calculated above. The circumference of the circle is given by C=2πa2. Now calculate the orbital speed of the Sun.