The problem with direct imaging
Angular resolution
Telescopes each have an ‘angular resolution’ which describes their ability to distinguish two points clearly from one another. An angular resolution of 1 degree means a telescope is able to clearly separate two points that are 1 degree apart from one another. The actual spatial distance this corresponds to varies depending on how far away the objects are from the observer e.g. if the objects were just 1m away, two points could be distinguished from one another even if they were only 2cm apart. However, if the objects were 380,000km away (the distance of the Moon from the Earth), we could only distinguish two points that were approximately 6,600km apart – this is equal to almost twice the diameter of the Moon itself! As you can tell, this would be a very poor angular resolution indeed, especially given the fact we can see the Moon clearly, with detail, with just our naked eye!
Fortunately, the resolutions of modern telescopes are far, far better than in the example above. The Hubble Space Telescope has an angular resolution of just 0.05 arcseconds, where an arcsecond is 1/60th of an arcminute and an arcminute is in turn 1/60th of a degree (therefore 1 arcsecond equals 1/3,600th of a degree).
Question
To prove the difficulties of direct imaging, try calculating whether a Jupiter sized planet (the largest in our solar system) would be resolvable by Hubble if it were orbiting Proxima Centauri, our nearest star. The following information is needed in the calculation:
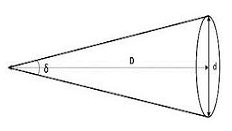
- The distance to Proxima Centauri (D) is 4.22 lightyears.
- 1 lightyear is approximately equal to 9,500,000,000,000,000 (9.5 × 1015) metres!
- The diameter of Jupiter (d) is approximately 140,000km.
- The angle (δ) subtended by Jupiter is approximately equal to 'd' divided by 'D', when δ is small, and when δ is given in ‘radians’.
- 1 radian = (360 ÷ 2π) degrees; 1 degree = (2π ÷ 360) radians.
For additional guidance see the relevant section in our guide linked near the top of the page.
